MATERI AJAR RABU, 20 AGUSTUS 2025

Hari / Tanggal       : Rabu, 20 Agustus 2025

Fase/Kelas              : C / VI

Mata Pelajaran       : Matematika, Bahasa Indonesia.

Matematika

Pada akhir fase C, peserta didik dapat menunjukkan pemahaman dan intuisi bilangan (number sense) pada bilangan cacah sampai 1.000.000. Mereka dapat membaca, menulis, menentukan nilai tempat, membandingkan, mengurutkan, melakukan komposisi dan dekomposisi bilangan tersebut. Mereka juga dapat menyelesaikan masalah yang berkaitan dengan uang. Mereka dapat melakukan operasi penjumlahan, pengurangan, perkalian, dan pembagian bilangan cacah sampai 100.000. Mereka juga dapat menyelesaikan masalah yang berkaitan dengan KPK dan FPB. Peserta didik dapat membandingkan dan mengurutkan berbagai pecahan termasuk pecahan campuran, melakukan operasi penjumlahan dan pengurangan pecahan, serta melakukan operasi perkalian dan pembagian pecahan dengan bilangan asli. Mereka dapat mengubah pecahan menjadi desimal, serta membandingkan dan mengurutkan bilangan desimal (satu angka di belakang koma)

Tujuan Pembelajaran : Murid dapat melakukan operasi hitung penjumlahan, pengurangan, perkalian dan pembagian pecahan.

Bahasa Indonesia

Capaian Pembelajaran: 

Peserta didik mampu menjelaskan kembali ide pokok dan beberapa ide pendukung dari teks informasional, berpartisipasi aktif dalam diskusi  dengan mempresentasikan gagasan, dan mampu menulis laporan sederhana (hasil wawancara) untuk menyampaikan informasi.

Tujuan Pembelajaran: 

Murid dapat :

1.  Memahami isi artikel tentang musisi Indonesia dan diplomasi budaya serta menjawab pertanyaan pemahaman.

2. Membuat peta pikiran untuk mengorganisasi gagasan tentang potensi diplomasi lunak Indonesia.

3. Merancang dan melakukan wawancara sederhana untuk menggali informasi tentang seni budaya lokal.

4. Menuliskan hasil wawancara dalam bentuk laporan singkat yang informatif

Assalamualaikum wr wb

Apa kabar anak sholih sholihah
Semoga semuanya dalam keadaan sehat wal'aafiyat
Jangan lupa sarapan dan persiapkan buku pelajaran kalian ya...
Mari awali kegiatan belajar hari ini dengan berdoa.

BAHASA INDONESIA

Pada pembelajaran Bahasa Indonesia kelas VI Kurikulum Merdeka terdapat pembahasan tentang Joey Alexander, Pianis yang Mendunia. Tujuan pembelajaran kali ini adalah peserta didik mampu menyimak dengan baik dan menjawab pertanyaan mengenai artikel yang dibacakan. Pada kegiatan ini pesera didik menjelaskan kembali ide pokok dan beberapa ide pendukung pada teks yang dibacakan berdasarkan pemahaman dan pemaknaannya terhadap tulisan dan gambar pendukung.

Gagasan pokok adalah ide utama dari sebuah paragraf. Gagasan pokok biasanya terdapat di kalimat utama, bisa diletakkan di kalimat pertama dan terakhir. Sementara itu, gagasan pendukung adalah penjelasan atau informasi lain yang memperkuat gagasan pokok.

Di dalam sebuah paragraf, gagasan pokok dan gagasan pendukung memiliki peranan yang penting. Agar lebih tahu fungsi dari masing-masing gagasan, berikut ini penjabaran lebih lengkap terkait gagasan pokok dan gagasan Pendukung.

Fungsi Gagasan Pokok

1. Sebagai pokok masalah dalam paragraf atau teks.
2. Menunjukkan informasi yang ingin disampaikan penulis.
3. Memudahkan pembaca untuk memahami maksud teks.
4. Sebagai batasan untuk penulis dalam mengembangkan paragraf. 

Fungsi Gagasan Pendukung

1. Sementara itu, untuk fungsi gagasan pendukung adalah sebagai berikut:
2. Menjelaskan gagasan pokok.
3. Melengkapi gagasan pokok.
4. Memberikan informasi tambahan yang masih berkaitan dengan gagasan pokok. 

Terdapat beberapa cara yang bisa kamu lakukan dalam menentukan gagasan pokok dan gagasan pendukung. Pertama-tama, tentu saja kamu harus membaca paragraf tersebut secara cermat dan utuh serta pahami maksud dari paragraf tersebut.

Teruslah membaca hingga kamu menemukan gagasan pokok dari paragraf tersebut. Gagasan pokok bisa diletakkan di awal atau akhir. Kemudian, cermati apakah kalimat tersebut merupakan gagasan pokok atau bukan. 

Setelah menemukan gagasan pokok, kamu bisa menganalisis gagasan pendukungnya. Selain bisa dilihat dari letak kalimatnya, kamu bisa mengidentifikasi kata-kata yang menggunakan kata ganti atau rujukan, seperti: ini, itu, tersebut, mereka, dan lainnya.

Jangan lupa tulis gagasan pokok dan gagasan pendukung yang sudah kamu temukan. Baca kembali apakah gagasan pokok dan gagasan pendukung yang kamu tulis sudah benar atau belum.

Menyimak

Bacalah dengan nyaring secara bergantian artikel tentang musisi Indonesia yang dikenal di panggung dunia. Sambil menyimak bacaan, catatlah sebanyak mungkin kata kunci atau informasi penting dan menarik di buku tulis kalian.

Sekarang, periksalah catatan kalian! Tugas kalian berikutnya adalah membuat pertanyaan dari informasi yang kalian catat. Kalian akan menanyakan pertanyaan tersebut kepada teman sebangku. Kalian juga harus menjawab pertanyaan teman sebangku kalian. Jangan lupa untuk menanyakan pertanyaan secara bergantian. Apabila pertanyaan teman kalian sama dengan pertanyaan yang telah kalian buat, kalian tidak dapat menanyakan pertanyaan itu lagi.

No.	Kata Kunci	Pertanyaanku
1.	Amerika	Di manakah Joey Alexander sekarang tinggal?
2.	Bali	Di manakah Joey Alexander dilahirkan?
3.	Keyboard Elektronik	Apa nama alat musik yang digunakan Joey saat mulai belajar bermain piano?
4.	Jaz klasik	Apa aliran musik yang dikenalkan ayah Joey?
5.	Herbie Hancock	Siapa nama pianis terkenal yang mengunjungi Indonesia saat Joey berusia 8 tahun?
6.	Ukraina	Di mana Joey memenangkan hadiah kompetisi musik untuk semua usia yang diikuti 200 peserta dari 17 negara?
7.	Trio Joey Alexander	Apa nama grup musik Joey sekarang?

Jumlah pertanyaan teman yang kujawab dengan benar: .....

Jumlah pertanyaan yang dijawab temanku dengan benar ....

Dengan membuat dan menjawab pertanyaan, kalian berlatih mengingat ide pokok dan ide pendukung pada teks yang dibacakan kepada kalian.

MATEMATIKA

1. Pecahan adalah bagian dari suatu kesatuan yang dibagi menjadi beberapa bagian yang sama besar. Pecahan terdiri dari dua bagian:

·        Pembilang (numerator): Angka yang ada di atas garis pecahan.

·        Penyebut (denominator): Angka yang ada di bawah garis pecahan.

Contoh:3/4

·        Pembilang = 3

·        Penyebut = 4

Ini berarti "3 dari 4 bagian yang sama besar."

2. Jenis-jenis Pecahan

Pecahan terbagi menjadi beberapa jenis, yaitu:

·        Pecahan Sejenis: Pecahan yang penyebutnya sama.

o   Contoh: 1/4, 3/4, 2/4

·        Pecahan Tak Sejenis: Pecahan yang penyebutnya berbeda.

o   Contoh: 1/4, 1/3, 1/2

·        Pecahan Campuran: Gabungan antara bilangan bulat dan pecahan.

o   Contoh: 1 1/2

·        Pecahan Desimal: Pecahan yang penyebutnya adalah kelipatan 10 (10, 100, 1000, dll).

o   Contoh: 0.5 (1/2), 0.75 (3/4)

3. Operasi pada Pecahan

A. Penjumlahan dan Pengurangan Pecahan Sejenis

Untuk penjumlahan atau pengurangan pecahan sejenis, hanya pembilang yang dijumlahkan atau dikurangkan, sedangkan penyebutnya tetap sama.

Contoh Penjumlahan Pecahan Sejenis:
1/4 + 2/4 = (1 + 2)/4 = 3/4

Contoh Pengurangan Pecahan Sejenis:
3/5 - 1/5 = (3 - 1)/5 = 2/5

B. Penjumlahan dan Pengurangan Pecahan Tak Sejenis

Untuk pecahan tak sejenis, kita harus mencari KPK (Kelipatan Persekutuan Terkecil) dari penyebut pecahan-pecahan tersebut, kemudian menyamakan penyebutnya.

Contoh Penjumlahan Pecahan Tak Sejenis:
1/3 + 1/4
Cari KPK dari 3 dan 4, yaitu 12.
1/3 = 4/12 dan 1/4 = 3/12.
Jadi, 4/12 + 3/12 = 7/12.

C. Perkalian dan Pembagian Pecahan

Rumus Cara Menghitung Perkalian dan Pembagian Pecahan

Gambar di atas adalah rumus perkalian dan pembagian bilangan pecahan. Untuk lebih jelasnya rumus tersebut dijabarkan pada pembahasan di bawah ini, simak video berikut :

                                                          VIDEO PEMBELAJARAN


Perkalian Sesama Bilangan Pecahan 

Untuk mengalikan bilangan pecahan biasa dengan bilangan pecahan biasa, caranya sangatlah mudah yaitu dengan mengalikan pembilang dengan pembilang lalu mengalikan penyebut dengan penyebut.
Perhatikan contoh berikut :





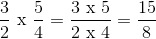
Perkalian Bilangan Pecahan Biasa dengan Bilangan BulatDalam menyelesaikan perkalian pecahan biasa dengan bilangan bulat, kalian cukup mengalikan pembilang dengan bilangan bulat tersebut, kemudian dibagi dengan penyebut.

Contoh :

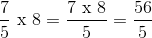
Pembagian Bilangan Pecahan Biasa 

Dalam menyelesaikan operasi pembagian bilangan pecahan biasa dengan pecahan biasa caranya cukup sederhana, yaitu dengan membalik pembilang dan penyebut dari salah satu bilangan pecahan tersebut, kemudian kedua bilangan pecahan tersebut dikalikan.
Perhatikan contoh berikut ini :





Kesimpulan dari pembahasan materi di atas adalah bahwa Cara Menghitung Perkalian dan Pembagian Bilangan Pecahan tidaklah begitu sulit untuk dipahami. Hanya dibutuhkan ketelitian dalam mengalikan angka - angka yang ada pada bilangan pecahan tersebut. Untuk menambah wawasan kalian mengenai materi bilangan pecahan, pelajari juga materi tentang Cara Mengubah Bilangan Pecahan Biasa Menjadi Bilangan Pecahan Campuran. Semoga artikel ini bisa membantu kalian dalam mengerjakan soal - soal yang berkaitan dengan bilangan pecahan.